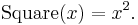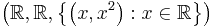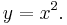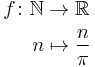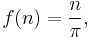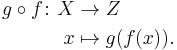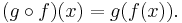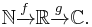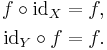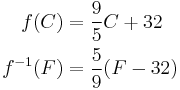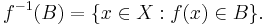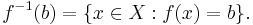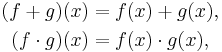Function (mathematics)
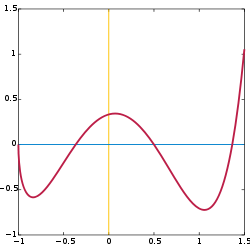
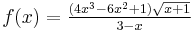
Both the domain and the range in the picture are the set of real numbers between -1 and 1.5.
The mathematical concept of a function expresses the intuitive idea that one quantity (the argument of the function, also known as the input) completely determines another quantity (the value, or the output). A function assigns a unique value to each input of a specified type. The argument and the value may be real numbers, but they can also be elements from any given sets: the domain and the codomain of the function. An example of a function with the real numbers as both its domain and codomain is the function f(x) = 2x, which assigns to every real number the real number with twice its value. In this case, it is written that f(5) = 10.
In addition to elementary functions on numbers, functions include maps between algebraic structures like groups and maps between geometric objects like manifolds. In the abstract set-theoretic approach, a function is a relation between the domain and the codomain that associates each element in the domain with exactly one element in the codomain. An example of a function with domain {A,B,C} and codomain {1,2,3} associates A with 1, B with 2, and C with 3.
There are many ways to describe or represent functions: by a formula, by an algorithm that computes it, by a plot or a graph. A table of values is a common way to specify a function in statistics, physics, chemistry, and other sciences. A function may also be described through its relationship to other functions, for example, as the inverse function or a solution of a differential equation. There are uncountably many different functions from the set of natural numbers to itself, most of which cannot be expressed with a formula or an algorithm.
In a setting where they have numerical outputs, functions may be added and multiplied, yielding new functions. Collections of functions with certain properties, such as continuous functions and differentiable functions, usually required to be closed under certain operations, are called function spaces and are studied as objects in their own right, in such disciplines as real analysis and complex analysis. An important operation on functions, which distinguishes them from numbers, is the composition of functions.
Overview
Because functions are so widely used, many traditions have grown up around their use. The symbol for the input to a function is often called the independent variable or argument and is often represented by the letter x or, if the input is a particular time, by the letter t. The symbol for the output is called the dependent variable or value and is often represented by the letter y. The function itself is most often called f, and thus the notation y = f(x) indicates that a function named f has an input named x and an output named y.
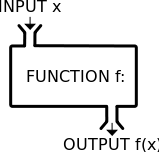
The set of all permitted inputs to a given function is called the domain of the function. The set of all resulting outputs is called the image or range of the function. The image is often a subset of some larger set, called the codomain of a function. Thus, for example, the function f(x) = x2 could take as its domain the set of all real numbers, as its image the set of all non-negative real numbers, and as its codomain the set of all real numbers. In that case, we would describe f as a real-valued function of a real variable. Sometimes, especially in computer science, the term "range" refers to the codomain rather than the image, so care needs to be taken when using the word.
It is usual practice in mathematics to introduce functions with temporary names like ƒ. For example, ƒ(x) = 2x+1, implies ƒ(3) = 7; when a name for the function is not needed, the form y = 2x+1 may be used. If a function is often used, it may be given a more permanent name as, for example,
Functions need not act on numbers: the domain and codomain of a function may be arbitrary sets. One example of a function that acts on non-numeric inputs takes English words as inputs and returns the first letter of the input word as output. Furthermore, functions need not be described by any expression, rule or algorithm: indeed, in some cases it may be impossible to define such a rule. For example, the association between inputs and outputs in a choice function often lacks any fixed rule, although each input element is still associated to one and only one output.
A function of two or more variables is considered in formal mathematics as having a domain consisting of ordered pairs or tuples of the argument values. For example Sum(x,y) = x+y operating on integers is the function Sum with a domain consisting of pairs of integers. Sum then has a domain consisting of elements like (3,4), a codomain of integers, and an association between the two that can be described by a set of ordered pairs like ((3,4), 7). Evaluating Sum(3,4) then gives the value 7 associated with the pair (3,4).
A family of objects indexed by a set is equivalent to a function. For example, the sequence 1, 1/2, 1/3, ..., 1/n, ... can be written as the ordered sequence <1/n> where n is a natural number, or as a function f(n) = 1/n from the set of natural numbers into the set of rational numbers.
Dually, a surjective function partitions its domain into disjoint sets indexed by the codomain. This partition is known as the kernel of the function, and the parts are called the fibers or level sets of the function at each element of the codomain. (A non-surjective function divides its domain into disjoint and possibly-empty subsets).
Definition
One precise definition of a function is that it consists of an ordered triple of sets, which may be written as (X, Y, F). X is the domain of the function, Y is the codomain, and F is a set of ordered pairs. In each of these ordered pairs (a, b), the first element a is from the domain, the second element b is from the codomain, and every element in the domain is the first element in one and only one ordered pair. The set of all b is known as the image of the function. Some authors use the term "range" to mean the image, others to mean the codomain.
The notation ƒ:X→Y indicates that ƒ is a function with domain X and codomain Y.
In most practical situations, the domain and codomain are understood from context, and only the relationship between the input and output is given. Thus
is usually written as
The graph of a function is its set of ordered pairs. Such a set can be plotted on a pair of coordinate axes; for example, (3, 9) is the point of intersection of the lines x = 3 and y = 9.
A function is a special case of a more general mathematical concept, the relation, for which the restriction that each element of the domain appear as the first element in one and only one ordered pair is removed (or, in other words, the restriction that each input be associated to exactly one output). A relation is "single-valued" or "functional" when for each element of the domain set, the graph contains at most one ordered pair (and possibly none) with it as a first element. A relation is called "left-total" or simply "total" when for each element of the domain, the graph contains at least one ordered pair with it as a first element (and possibly more than one). A relation that is both left-total and single-valued is a function.
In some parts of mathematics, including recursion theory and functional analysis, it is convenient to study partial functions in which some values of the domain have no association in the graph; i.e., single-valued relations. For example, the function f such that f(x) = 1/x does not define a value for x = 0, and so is only a partial function from the real line to the real line. The term total function can be used to stress the fact that every element of the domain does appear as the first element of an ordered pair in the graph. In other parts of mathematics, non-single-valued relations are similarly conflated with functions: these are called multivalued functions, with the corresponding term single-valued function for ordinary functions.
Some authors (especially in set theory) define a function as simply its graph f, with the restriction that the graph should not contain two distinct ordered pairs with the same first element. Indeed, given such a graph, one can construct a suitable triple by taking the set of all first elements as the domain and the set of all second elements as the codomain: this automatically causes the function to be total and surjective . However, most authors in advanced mathematics outside of set theory prefer the greater power of expression afforded by defining a function as an ordered triple of sets.
Many operations in set theory—such as the power set—have the class of all sets as their domain, therefore, although they are informally described as functions, they do not fit the set-theoretical definition above outlined.
Vocabulary
A specific input in a function is called an argument of the function. For each argument value x, the corresponding unique y in the codomain is called the function value at x, output of ƒ for an argument x, or the image of x under ƒ. The image of x may be written as ƒ(x) or as y.
The graph of a function ƒ is the set of all ordered pairs (x, ƒ(x)), for all x in the domain X. If X and Y are subsets of R, the real numbers, then this definition coincides with the familiar sense of "graph" as a picture or plot of the function, with the ordered pairs being the Cartesian coordinates of points.
A function can also be called a map or a mapping. Some authors, however, use the terms "function" and "map" to refer to different types of functions. Other specific types of functions include functionals and operators.
Notation
Formal description of a function typically involves the function's name, its domain, its codomain, and a rule of correspondence. Thus we frequently see a two-part notation, an example being
where the first part is read:
- "ƒ is a function from N to R" (one often writes informally "Let ƒ: X → Y" to mean "Let ƒ be a function from X to Y"), or
- "ƒ is a function on N into R", or
- "ƒ is an R-valued function of an N-valued variable",
and the second part is read:
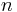 maps to
maps to 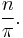
Here the function named "ƒ" has the natural numbers as domain, the real numbers as codomain, and maps n to itself divided by π. Less formally, this long form might be abbreviated
where f(n) is read as "f as function of n" or "f of n". There is some loss of information: we no longer are explicitly given the domain N and codomain R.
It is common to omit the parentheses around the argument when there is little chance of confusion, thus: sin x; this is known as prefix notation. Writing the function after its argument, as in x ƒ, is known as postfix notation; for example, the factorial function is customarily written n!, even though its generalization, the gamma function, is written Γ(n). Parentheses are still used to resolve ambiguities and denote precedence, though in some formal settings the consistent use of either prefix or postfix notation eliminates the need for any parentheses.
Functions with multiple inputs and outputs
The concept of function can be extended to an object that takes a combination of two (or more) argument values to a single result. This intuitive concept is formalized by a function whose domain is the Cartesian product of two or more sets.
For example, consider the function that associates two integers to their product: ƒ(x, y) = x·y. This function can be defined formally as having domain Z×Z , the set of all integer pairs; codomain Z; and, for graph, the set of all pairs ((x,y), x·y). Note that the first component of any such pair is itself a pair (of integers), while the second component is a single integer.
The function value of the pair (x,y) is ƒ((x,y)). However, it is customary to drop one set of parentheses and consider ƒ(x,y) a function of two variables, x and y. Functions of two variables may be plotted on the three-dimensional Cartesian as ordered triples of the form (x,y,f(x,y)).
The concept can still further be extended by considering a function that also produces output that is expressed as several variables. For example, consider the function swap(x, y) = (y, x) with domain R×R and codomain R×R as well. The pair (y, x) is a single value in the codomain seen as a Cartesian product.
Currying
An alternative approach to handling functions with multiple arguments is to transform them into a chain of functions that each takes a single argument. For instance, one can interpret Add(3,5) to mean "first produce a function that adds 3 to its argument, and then apply the 'Add 3' function to 5". This transformation is called currying: Add 3 is curry(Add) applied to 3. There is a bijection between the function spaces CA×B and (CB)A.
When working with curried functions it is customary to use prefix notation with function application considered left-associative, since juxtaposition of multiple arguments—as in (ƒ x y)—naturally maps to evaluation of a curried function. Conversely, the → and ⟼ symbols are considered to be right-associative, so that curried functions may be defined by a notation such as ƒ: Z → Z → Z = x ⟼ y ⟼ x·y
Binary operations
The familiar binary operations of arithmetic, addition and multiplication, can be viewed as functions from R×R to R. This view is generalized in abstract algebra, where n-ary functions are used to model the operations of arbitrary algebraic structures. For example, an abstract group is defined as a set X and a function ƒ from X×X to X that satisfies certain properties.
Traditionally, addition and multiplication are written in the infix notation: x+y and x×y instead of +(x, y) and ×(x, y).
Injective and surjective functions
Three important kinds of function are the injections (or one-to-one functions), which have the property that if ƒ(a) = ƒ(b) then a must equal b; the surjections (or onto functions), which have the property that for every y in the codomain there is an x in the domain such that ƒ(x) = y; and the bijections, which are both one-to-one and onto. This nomenclature was introduced by the Bourbaki group.
When the definition of a function by its graph only is used, since the codomain is not defined, the "surjection" must be accompanied with a statement about the set the function maps onto. For example, we might say ƒ maps onto the set of all real numbers.
Function composition

The function composition of two or more functions takes the output of one or more functions as the input of others. The functions ƒ: X → Y and g: Y → Z can be composed by first applying ƒ to an argument x to obtain y = ƒ(x) and then applying g to y to obtain z = g(y). The composite function formed in this way from general ƒ and g may be written
This notation follows the form such that
The function on the right acts first and the function on the left acts second, reversing English reading order. We remember the order by reading the notation as "g of ƒ". The order is important, because rarely do we get the same result both ways. For example, suppose ƒ(x) = x2 and g(x) = x+1. Then g(ƒ(x)) = x2+1, while ƒ(g(x)) = (x+1)2, which is x2+2x+1, a different function.
In a similar way, the function given above by the formula y = 5x−20x3+16x5 can be obtained by composing several functions, namely the addition, negation, and multiplication of real numbers.
An alternative to the colon notation, convenient when functions are being composed, writes the function name above the arrow. For example, if ƒ is followed by g, where g produces the complex number eix, we may write
A more elaborate form of this is the commutative diagram.
Identity function
The unique function over a set X that maps each element to itself is called the identity function for X, and typically denoted by idX. Each set has its own identity function, so the subscript cannot be omitted unless the set can be inferred from context. Under composition, an identity function is "neutral": if ƒ is any function from X to Y, then
Restrictions and extensions
Informally, a restriction of a function ƒ is the result of trimming its domain.
More precisely, if ƒ is a function from a X to Y, and S is any subset of X, the restriction of ƒ to S is the function ƒ|S from S to Y such that ƒ|S(s) = ƒ(s) for all s in S.
If g is a restriction of ƒ, then it is said that ƒ is an extension of g.
The overriding of f: X → Y by g: W → Y (also called overriding union) is an extension of g denoted as (f ⊕ g): (X ∪ W) → Y. Its graph is the set-theoretical union of the graphs of g and f|X \ W. Thus, it relates any element of the domain of g to its image under g, and any other element of the domain of f to its image under f. Overriding is an associative operation; it has the empty function as an identity element. If f|X ∩ W and g|X ∩ W are pointwise equal (e.g., the domains of f and g are disjoint), then the union of f and g is defined and is equal to their overriding union. This definition agrees with the definition of union for binary relations.
Inverse function
If ƒ is a function from X to Y then an inverse function for ƒ, denoted by ƒ−1, is a function in the opposite direction, from Y to X, with the property that a round trip (a composition) returns each element to itself. Not every function has an inverse; those that do are called invertible. The inverse function exists if and only if ƒ is a bijection.
As a simple example, if ƒ converts a temperature in degrees Celsius C to degrees Fahrenheit F, the function converting degrees Fahrenheit to degrees Celsius would be a suitable ƒ−1.
The notation for composition is similar to multiplication; in fact, sometimes it is denoted using juxtaposition, gƒ, without an intervening circle. With this analogy, identity functions are like the multiplicative identity, 1, and inverse functions are like reciprocals (hence the notation).
For functions that are injections or surjections, generalized inverse functions can be defined, called left and right inverses respectively. Left inverses map to the identity when composed to the left; right inverses when composed to the right.
Image of a set
The concept of the image can be extended from the image of a point to the image of a set. If A is any subset of the domain, then ƒ(A) is the subset of im ƒ consisting of all images of elements of A. We say the ƒ(A) is the image of A under f.
Use of ƒ(A) to denote the image of a subset A⊆X is consistent so long as no subset of the domain is also an element of the domain. In some fields (e.g., in set theory, where ordinals are also sets of ordinals) it is convenient or even necessary to distinguish the two concepts; the customary notation is ƒ[A] for the set { ƒ(x): x ∈ A }; some authors write ƒ`x instead of ƒ(x), and ƒ``A instead of ƒ[A].
Notice that the image of ƒ is the image ƒ(X) of its domain, and that the image of ƒ is a subset of its codomain.
Inverse image
The inverse image (or preimage, or more precisely, complete inverse image) of a subset B of the codomain Y under a function ƒ is the subset of the domain X defined by
So, for example, the preimage of {4, 9} under the squaring function is the set {−3,−2,2,3}.
In general, the preimage of a singleton set (a set with exactly one element) may contain any number of elements. For example, if ƒ(x) = 7, then the preimage of {5} is the empty set but the preimage of {7} is the entire domain. Thus the preimage of an element in the codomain is a subset of the domain. The usual convention about the preimage of an element is that ƒ−1(b) means ƒ−1({b}), i.e
In the same way as for the image, some authors use square brackets to avoid confusion between the inverse image and the inverse function. Thus they would write ƒ−1[B] and ƒ−1[b] for the preimage of a set and a singleton.
The preimage of a singleton set is sometimes called a fiber. The term kernel can refer to a number of related concepts.
Specifying a function
A function can be defined by any mathematical condition relating each argument to the corresponding output value. If the domain is finite, a function ƒ may be defined by simply tabulating all the arguments x and their corresponding function values ƒ(x). More commonly, a function is defined by a formula, or (more generally) an algorithm — a recipe that tells how to compute the value of ƒ(x) given any x in the domain.
There are many other ways of defining functions. Examples include piecewise definitions, induction or recursion, algebraic or analytic closure, limits, analytic continuation, infinite series, and as solutions to integral and differential equations. The lambda calculus provides a powerful and flexible syntax for defining and combining functions of several variables.
Computability
Functions that send integers to integers, or finite strings to finite strings, can sometimes be defined by an algorithm, which gives a precise description of a set of steps for computing the output of the function from its input. Functions definable by an algorithm are called computable functions. For example, the Euclidean algorithm gives a precise process to compute the greatest common divisor of two positive integers. Many of the functions studied in the context of number theory are computable.
Fundamental results of computability theory show that there are functions that can be precisely defined but are not computable. Moreover, in the sense of cardinality, almost all functions from the integers to integers are not computable. The number of computable functions from integers to integers is countable, because the number of possible algorithms is. The number of all functions from integers to integers is higher: the same as the cardinality of the real numbers. Thus most functions from integers to integers are not computable. Specific examples of uncomputable functions are known, including the busy beaver function and functions related to the halting problem and other undecidable problems.
Function spaces
The set of all functions from a set X to a set Y is denoted by X → Y, by [X → Y], or by YX.
The latter notation is motivated by the fact that, when X and Y are finite and of size |X| and |Y|, then the number of functions X → Y is |YX| = |Y||X|. This is an example of the convention from enumerative combinatorics that provides notations for sets based on their cardinalities. Other examples are the multiplication sign X×Y used for the Cartesian product, where |X×Y| = |X|·|Y|; the factorial sign X!, used for the set of permutations where |X!| = |X|!; and the binomial coefficient sign 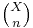 , used for the set of n-element subsets where
, used for the set of n-element subsets where 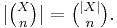
If ƒ: X → Y, it may reasonably be concluded that ƒ ∈ [X → Y].
Pointwise operations
If ƒ: X → R and g: X → R are functions with a common domain of X and common codomain of a ring R, then the sum function ƒ + g: X → R and the product function ƒ ⋅ g: X → R can be defined as follows:
for all x in X.
This turns the set of all such functions into a ring. The binary operations in that ring have as domain ordered pairs of functions, and as codomain functions. This is an example of climbing up in abstraction, to functions of more complex types.
By taking some other algebraic structure A in the place of R, we can turn the set of all functions from X to A into an algebraic structure of the same type in an analogous way.
Other properties
There are many other special classes of functions that are important to particular branches of mathematics, or particular applications. Here is a partial list:
|
|
|
History
Functions prior to Leibniz
- Historically, some mathematicians can be regarded as having foreseen and come close to a modern formulation of the concept of function. Among them is Oresme (1323-1382) . . . In his theory, some general ideas about independent and dependent variable quantities seem to be present.[1][2]
Ponte further notes that "The emergence of a notion of function as an individualized mathematical entity can be traced to the beginnings of infinitesimal calculus".[1]
The notion of "function" in analysis
As a mathematical term, "function" was coined by Gottfried Leibniz, in a 1673 letter, to describe a quantity related to a curve, such as a curve's slope at a specific point.[3][4] The functions Leibniz considered are today called differentiable functions. For this type of function, one can talk about limits and derivatives; both are measurements of the output or the change in the output as it depends on the input or the change in the input. Such functions are the basis of calculus.
Johann Bernoulli "by 1718, had come to regard a function as any expression made up of a variable and some constants",[5] and Leonhard Euler during the mid-18th century used the word to describe an expression or formula involving variables and constants e.g., x2+3x+2.[6]
Alexis Claude Clairaut (in approximately 1734) and Euler introduced the familiar notation " f(x) ".[6]
At first, the idea of a function was rather limited. Joseph Fourier, for example, claimed that every function had a Fourier series, something no mathematician would claim today. By broadening the definition of functions, mathematicians were able to study "strange" mathematical objects such as continuous functions that are nowhere differentiable. These functions were first thought to be only theoretical curiosities, and they were collectively called "monsters" as late as the turn of the 20th century. However, powerful techniques from functional analysis have shown that these functions are, in a precise sense, more common than differentiable functions. Such functions have since been applied to the modeling of physical phenomena such as Brownian motion.
During the 19th century, mathematicians started to formalize all the different branches of mathematics. Weierstrass advocated building calculus on arithmetic rather than on geometry, which favoured Euler's definition over Leibniz's (see arithmetization of analysis).
Dirichlet and Lobachevsky are traditionally credited with independently giving the modern "formal" definition of a function as a relation in which every first element has a unique second element. Eves asserts that "the student of mathematics usually meets the Dirichlet definition of function in his introductory course in calculus,[7] but Dirichlet's claim to this formalization is disputed by Imre Lakatos:
- There is no such definition in Dirichlet's works at all. But there is ample evidence that he had no idea of this concept. In his [1837], for instance, when he discusses piecewise continuous functions, he says that at points of discontinuity the function has two values: ...
- (Proofs and Refutations, 151, Cambridge University Press 1976.)
In the context of "the Differential Calculus" George Boole defined (circa 1849) the notion of a function as follows:
- "That quantity whose variation is uniform . . . is called the independent variable. That quantity whose variation is referred to the variation of the former is said to be a function of it. The Differential calculus enables us in every case to pass from the function to the limit. This it does by a certain Operation. But in the very Idea of an Operation is . . . the idea of an inverse operation. To effect that inverse operation in the present instance is the business of the Int[egral] Calculus."[8]
The logician's "function" prior to 1850
Logicians of this time were primarily involved with analyzing syllogisms (the 2000 year-old Aristotelian forms and otherwise), or as Augustus De Morgan (1847) stated it: "the examination of that part of reasoning which depends upon the manner in which inferences are formed, and the investigation of general maxims and rules for constructing arguments".[9] At this time the notion of (logical) "function" is not explicit, but at least in the work of De Morgan and George Boole it is implied: we see abstraction of the argument forms, the introduction of variables, the introduction of a symbolic algebra with respect to these variables, and some of the notions of set theory.
De Morgan's 1847 "FORMAL LOGIC OR, The Calculus of Inference, Necessary and Probable" observes that "[a] logical truth depends upon the structure of the statement, and not upon the particular matters spoken of"; he wastes no time (preface page i) abstracting: "In the form of the proposition, the copula is made as absract as the terms". He immediately (p. 1) casts what he calls "the proposition" (present-day propositional function or relation) into a form such as "X is Y", where the symbols X, "is", and Y represent, respectively, the subject, copula, and predicate. While the word "function" does not appear, the notion of "abstraction" is there, "variables" are there, the notion of inclusion in his symbolism “all of the Δ is in the О” (p. 9) is there, and lastly a new symbolism for logical analysis of the notion of "relation" (he uses the word with respect to this example " X)Y " (p. 75) ) is there:
- " A1 X)Y To take an X it is necessary to take a Y" [or To be an X it is necessary to be a Y]
- " A1 Y)X To take an Y it is sufficient to take a X" [or To be a Y it is sufficient to be an X], etc.
In his 1848 The Nature of Logic Boole asserts that "logic . . . is in a more especial sense the science of reasoning by signs", and he briefly discusses the notions of "belonging to" and "class": "An individual may possess a great variety of attributes and thus belonging to a great variety of different classes" .[10] Like De Morgan he uses the notion of "variable" drawn from analysis; he gives an example of "represent[ing] the class oxen by x and that of horses by y and the conjunction and by the sign + . . . we might represent the aggregate class oxen and horses by x + y".[11]
The logicians' "function" 1850-1950
Eves observes "that logicians have endeavored to push down further the starting level of the definitional development of mathematics and to derive the theory of sets, or classes, from a foundation in the logic of propositions and propositional functions".[12] But by the late 19th century the logicians' research into the foundations of mathematics was undergoing a major split. The direction of the first group, the Logicists, can probably be summed up best by Bertrand Russell 1903:9 -- "to fulfil two objects, first, to show that all mathematics follows from symbolic logic, and secondly to discover, as far as possible, what are the principles of symbolic logic itself."
The second group of logicians, the set-theorists, emerged with Georg Cantor's "set theory" (1870–1890) but were driven forward partly as a result of Russell's discovery of a paradox that could be derived from Frege's conception of "function", but also as a reaction against Russell's proposed solution.[13] Zermelo's set-theoretic response was his 1908 Investigations in the foundations of set theory I -- the first axiomatic set theory; here too the notion of "propositional function" plays a role.
George Boole's The Laws of Thought 1854; John Venn's Symbolic Logic 1881
In his An Investigation into the laws of thought Boole now defined a function in terms of a symbol x as follows:
- "8. Definition.-- Any algebraic expression involving symbol x is termed a function of x, and may be represented by the abbreviated form f(x)"[14]
Boole then used algebraic expressions to define both algebraic and logical notions, e.g., 1−x is logical NOT(x), xy is the logical AND(x,y), x + y is the logical OR(x, y), x(x+y) is xx+xy, and "the special law" xx = x2 = x.[15]
In his 1881 Symbolic Logic Venn was using the words "logical function" and the contemporary symbolism ( x = f(y), y = f−1(x), cf page xxi) plus the circle-diagrams historically associated with Venn to describe "class relations",[16] the notions "'quantifying' our predicate", "propositions in respect of their extension", "the relation of inclusion and exclusion of two classes to one another", and "propositional function" (all on p. 10), the bar over a variable to indicate not-x (page 43), etc. Indeed he equated unequivocally the notion of "logical function" with "class" [modern "set"]: "... on the view adopted in this book, f(x) never stands for anything but a logical class. It may be a compound class aggregated of many simple classes; it may be a class indicated by certain inverse logical operations, it may be composed of two groups of classes equal to one another, or what is the same thing, their difference declared equal to zero, that is, a logical equation. But however composed or derived, f(x) with us will never be anything else than a general expression for such logical classes of things as may fairly find a place in ordinary Logic".[17]
Frege's Begriffsschrift 1879
Gottlob Frege's Begriffsschrift (1879) preceded Giuseppe Peano (1889), but Peano had no knowledge of Frege 1879 until after he had published his 1889.[18] Both writers strongly influenced Bertrand Russell (1903). Russell in turn influenced much of 20th-century mathematics and logic through his Principia Mathematica (1913) jointly authored with Alfred North Whitehead.
At the outset Frege abandons the traditional "concepts subject and predicate", replacing them with argument and function respectively, which he believes "will stand the test of time. It is easy to see how regarding a content as a function of an argument leads to the formation of concepts. Furthermore, the demonstration of the connection between the meanings of the words if, and, not, or, there is, some, all, and so forth, deserves attention".[19]
Frege begins his discussion of "function" with an example: Begin with the expression[20] "Hydrogen is lighter than carbon dioxide". Now remove the sign for hydrogen (i.e., the word "hydrogen") and replace it with the sign for oxygen (i.e., the word "oxygen"); this makes a second statement. Do this again (using either statement) and substitute the sign for nitrogen (i.e., the word "nitrogen") and note that "This changes the meaning in such a way that "oxygen" or "nitrogen" enters into the relations in which "hydrogen" stood before".[21] There are three statements:
- "Hydrogen is lighter than carbon dioxide."
- "Oxygen is lighter than carbon dioxide."
- "Nitrogen is lighter than carbon dioxide."
Now observe in all three a "stable component, representing the totality of [the] relations";[22] call this the function, i.e.,
- "... is lighter than carbon dioxide", is the function.
Frege calls the argument of the function "[t]he sign [e.g., hydrogen, oxygen, or nitrogen], regarded as replaceable by others that denotes the object standing in these relations".[23] He notes that we could have derived the function as "Hydrogen is lighter than . . .." as well, with an argument position on the right; the exact observation is made by Peano (see more below). Finally, Frege allows for the case of two (or more arguments). For example, remove "carbon dioxide" to yield the invariant part (the function) as:
- "... is lighter than ... "
The one-argument function Frege generalizes into the form Φ(A) where A is the argument and Φ( ) represents the function, whereas the two-argument function he symbolizes as Ψ(A, B) with A and B the arguments and Ψ( , ) the function and cautions that "in general Ψ(A, B) differs from Ψ(B, A)". Using his unique symbolism he translates for the reader the following symbolism:
- "We can read |--- Φ(A) as "A has the property Φ. |--- Ψ(A, B) can be translated by "B stands in the relation Ψ to A" or "B is a result of an application of the procedure Ψ to the object A".[24]
Peano 1889 The Principles of Arithmetic 1889
Peano defined the notion of "function" in a manner somewhat similar to Frege, but without the precision.[25] First Peano defines the sign "K means class, or aggregate of objects",[26] the objects of which satisfy three simple equality-conditions,[27] a = a, (a = b) = (b = a), IF ((a = b) AND (b = c)) THEN (a = c). He then introduces φ, "a sign or an aggregate of signs such that if x is an object of the class s, the expression φx denotes a new object". Peano adds two conditions on these new objects: First, that the three equality-conditions hold for the objects φx; secondly, that "if x and y are objects of class s and if x = y, we assume it is possible to deduce φx = φy".[28] Given all these conditions are met, φ is a "function presign". Likewise he identifies a "function postsign". For example if φ is the function presign a+, then φx yields a+x, or if φ is the function postsign +a then xφ yields x+a.[29]
Bertrand Russell's The Principles of Mathematics 1903
While the influence of Cantor and Peano was paramount,[30] in Appendix A "The Logical and Arithmetical Doctrines of Frege" of The Principles of Mathematics, Russell arrives at a discussion of Frege's notion of function, "...a point in which Frege's work is very important, and requires careful examination".[31] In response to his 1902 exchange of letters with Frege about the contradiction he discovered in Frege's Begriffsschrift Russell tacked this section on at the last moment.
For Russell the bedeviling notion is that of "variable": "6. Mathematical propositions are not only characterized by the fact that they assert implications, but also by the fact that they contain variables. The notion of the variable is one of the most difficult with which logic has to deal. For the present, I openly wish to make it plain that there are variables in all mathematical propositions, even where at first sight they might seem to be absent. . . . We shall find always, in all mathematical propositions, that the words any or some occur; and these words are the marks of a variable and a formal implication".[32]
As expressed by Russell "the process of transforming constants in a proposition into variables leads to what is called generalization, and gives us, as it were, the formal essence of a proposition ... So long as any term in our proposition can be turned into a variable, our proposition can be generalized; and so long as this is possible, it is the business of mathematics to do it";[33] these generalizations Russell named propositional functions".[34] Indeed he cites and quotes from Frege's Begriffsschrift and presents a vivid example from Frege's 1891 Function und Begriff: That "the essence of the arithmetical function 2*x3+x is what is left when the x is taken away, i.e., in the above instance 2*( )3 + ( ). The argument x does not belong to the function but the two taken together make the whole".[31] Russell agreed with Frege's notion of "function" in one sense: "He regards functions -- and in this I agree with him -- as more fundamental than predicates and relations" but Russell rejected Frege's "theory of subject and assertion", in particular "he thinks that, if a term a occurs in a proposition, the proposition can always be analysed into a and an assertion about a".[31]
Evolution of Russell's notion of "function" 1908-1913
Russell would carry his ideas forward in his 1908 Mathematical logical as based on the theory of types and into his and Whitehead's 1910-1913 Principia Mathematica. By the time of Principia Mathematica Russell, like Frege, considered the propositional function fundamental: "Propositional functions are the fundamental kind from which the more usual kinds of function, such as “sin ‘’x’’ or log x or "the father of x" are derived. These derivative functions . . . are called “descriptive functions". The functions of propositions . . . are a particular case of propositional functions".[35]
Propositional functions: Because his terminology is different from the contemporary, the reader may be confused by Russell's "propositional function". An example may help. Russell writes a propositional function in its raw form, e.g., as φŷ: "ŷ is hurt". (Observe the circumflex or "hat" over the variable y). For our example, we will assign just 4 values to the variable ŷ: "Bob", "This bird", "Emily the rabbit", and "y". Substitution of one of these values for variable ŷ yields a proposition; this proposition is called a "value" of the propositional function. In our example there are four values of the propositional function, e.g., "Bob is hurt", "This bird is hurt", "Emily the rabbit is hurt" and "y is hurt." A proposition, if it is significant—i.e., if its truth is determinate—has a truth-value of truth or falsity. If a proposition's truth value is "truth" then the variable's value is said to satisfy the propositional function. Finally, per Russell's definition, "a class [set] is all objects satisfying some propositional function" (p. 23). Note the word "all'" -- this is how the contemporary notions of "For all ∀" and "there exists at least one instance ∃" enter the treatment (p. 15).
To continue the example: Suppose (from outside the mathematics/logic) one determines that the propositions "Bob is hurt" has a truth value of "falsity", "This bird is hurt" has a truth value of "truth", "Emily the rabbit is hurt" has an indeterminate truth value because "Emily the rabbit" doesn't exist, and "y is hurt" is ambiguous as to its truth value because the argument y itself is ambiguous. While the two propositions "Bob is hurt" and "This bird is hurt" are significant (both have truth values), only the value "This bird" of the variable ŷ satisfies' the propositional function φŷ: "ŷ is hurt". When one goes to form the class α: φŷ: "ŷ is hurt", only "This bird" is included, given the four values "Bob", "This bird", "Emily the rabbit" and "y" for variable ŷ and their respective truth-values: falsity, truth, indeterminate, ambiguous.
Russell defines functions of propositions with arguments, and truth-functions f(p).[36] For example, suppose one were to form the "function of propositions with arguments" p1: "NOT(p) AND q" and assign its variables the values of p: "Bob is hurt" and q: "This bird is hurt". (We are restricted to the logical linkages NOT, AND, OR and IMPLIES, and we can only assign "significant" propositions to the variables p and q). Then the "function of propositions with arguments" is p1: NOT("Bob is hurt") AND "This bird is hurt"). To determine the truth value of this "function of propositions with arguments" we submit it to a "truth function", e.g., f(p1): f( NOT("Bob is hurt") AND "This bird is hurt") ), which yields a truth value of "truth".
The notion of a "many-one" functional relation": Russell first discusses the notion of "identity", then defines a descriptive function (pages 30ff) as the unique value ιx that satisfies the (2-variable) propositional function (i.e., "relation") φŷ.
- N.B. The reader should be warned here that the order of the variables are reversed! y is the independent variable and x is the dependent variable, e.g., x = sin(y).[37]
Russell symbolizes the descriptive function as "the object standing in relation to y": R'y =DEF (ιx)(x R y). Russell repeats that "R'y is a function of y, but not a propositional function [sic]; we shall call it a descriptive function. All the ordinary functions of mathematics are of this kind. Thus in our notation "sin y" would be written " sin 'y ", and "sin" would stand for the relation sin 'y has to y".[38]
Hardy 1908
Hardy 1908, pp. 26–28 defined a function as a relation between two variables x and y such that "to some values of x at any rate correspond values of y." He neither required the function to be defined for all values of x nor to associate each value of x to a single value of y. This broad definition of a function encompasses more relations than are ordinarily considered functions in contemporary mathematics.
The Formalist's "function": David Hilbert's axiomatization of mathematics (1904-1927)
David Hilbert set himself the goal of "formalizing" classical mathematics "as a formal axiomatic theory, and this theory shall be proved to be consistent, i.e., free from contradiction" .[39] In his 1927 The Foundations of Mathematics Hilbert frames the notion of function in terms of the existence of an "object":
- 13. A(a) --> A(ε(A)) Here ε(A) stands for an object of which the proposition A(a) certainly holds if it holds of any object at all; let us call ε the logical ε-function".[40] [The arrow indicates “implies”.]
Hilbert then illustrates the three ways how the ε-function is to be used, firstly as the "for all" and "there exists" notions, secondly to represent the "object of which [a proposition] holds", and lastly how to cast it into the choice function.
Recursion theory and computability: But the unexpected outcome of Hilbert's and his student Bernays's effort was failure; see Gödel's incompleteness theorems of 1931. At about the same time, in an effort to solve Hilbert's Entscheidungsproblem, mathematicians set about to define what was meant by an "effectively calculable function" (Alonzo Church 1936), i.e., "effective method" or "algorithm", that is, an explicit, step-by-step procedure that would succeed in computing a function. Various models for algorithms appeared, in rapid succession, including Church's lambda calculus (1936), Stephen Kleene's μ-recursive functions(1936) and Allan Turing's (1936-7) notion of replacing human "computers" with utterly-mechanical "computing machines" (see Turing machines). It was shown that all of these models could compute the same class of computable functions. Church's thesis holds that this class of functions exhausts all the number-theoretic functions that can be calculated by an algorithm. The outcomes of these efforts were vivid demonstrations that, in Turing's words, "there can be no general process for determining whether a given formula U of the functional calculus K [Principia Mathematica] is provable";[41] see more at Independence (mathematical logic) and Computability theory.
Development of the set-theoretic definition of "function"
Set theory began with the work of the logicians with the notion of "class" (modern "set") for example De Morgan (1847), Jevons (1880), Venn 1881, Frege 1879 and Peano (1889). It was given a push by Georg Cantor's attempt to define the infinite in set-theoretic treatment(1870–1890) and a subsequent discovery of an antinomy (contradiction, paradox) in this treatment (Cantor's paradox), by Russell's discovery (1902) of an antinomy in Frege's 1879 (Russell's paradox), by the discovery of more antinomies in the early 20th century (e.g., the 1897 Burali-Forti paradox and the 1905 Richard paradox), and by resistance to Russell's complex treatment of logic[42] and dislike of his axiom of reducibility[43] (1908, 1910–1913) that he proposed as a means to evade the antinomies.
Russell's paradox 1902
In 1902 Russell sent a letter to Frege pointing out that Frege's 1879 Begriffsschrift allowed a function to be an argument of itself: "On the other hand, it may also be that the argument is determinate and the function indeterminate . . .."[44] From this unconstrained situation Russell was able to form a paradox:
- "You state ... that a function, too, can act as the indeterminate element. This I formerly believed, but now this view seems doubtful to me because of the following contradiction. Let w be the predicate: to be a predicate that cannot be predicated of itself. Can w be predicated of itself?"[45]
Frege responded promptly that "Your discovery of the contradiction caused me the greatest surprise and, I would almost say, consternation, since it has shaken the basis on which I intended to build arithmetic".[46]
From this point forward development of the foundations of mathematics became an exercise in how to dodge "Russell's paradox", framed as it was in "the bare [set-theoretic] notions of set and element".[47]
Zermelo's set theory (1908) modified by Skolem (1922)
The notion of "function" appears as Zermelo's axiom III—the Axiom of Separation (Axiom der Aussonderung). This axiom constrains us to use a propositional function Φ(x) to "separate" a subset MΦ from a previously formed set M:
- "AXIOM III. (Axiom of separation). Whenever the propositional function Φ(x) is definite for all elements of a set M, M possesses a subset MΦ containing as elements precisely those elements x of M for which Φ(x) is true".[48]
As there is no universal set—sets originate by way of Axiom II from elements of (non-set) domain B -- "...this disposes of the Russell antinomy so far as we are concerned".[49] But Zermelo's "definite criterion" is imprecise, and is fixed by Weyl, Fraenkel, Skolem, and von Neumann.[50]
In fact Skolem in his 1922 referred to this "definite criterion" or "property" as a "definite proposition":
- "... a finite expression constructed from elementary propositions of the form a ε b or a = b by means of the five operations [logical conjunction, disjunction, negation, universal quantification, and existential quantification].[51]
van Heijenoort summarizes:
- "A property is definite in Skolem's sense if it is expressed . . . by a well-formed formula in the simple predicate calculus of first order in which the sole predicate constants are ε and possibly, =. ... Today an axiomatization of set theory is usually embedded in a logical calculus, and it is Weyl's and Skolem's approach to the formulation of the axiom of separation that is generally adopted.[52]
In this quote the reader may observe a shift in terminology: nowhere is mentioned the notion of "propositional function", but rather one sees the words "formula", "predicate calculus", "predicate", and "logical calculus." This shift in terminology is discussed more in the section that covers "function" in contemporary set theory.
The Wiener–Hausdorff–Kuratowski "ordered pair" definition 1914–1921
The history of the notion of "ordered pair" is not clear. As noted above, Frege (1879) proposed an intuitive ordering in his definition of a two-argument function Ψ(A, B). Norbert Wiener in his 1914 (see below) observes that his own treatment essentially "revert(s) to Schröder's treatment of a relation as a class of ordered couples".[53] Russell (1903) considered the definition of a relation (such as Ψ(A, B)) as a "class of couples" but rejected it:
- "There is a temptation to regard a relation as definable in extension as a class of couples. This is the formal advantage that it avoids the necessity for the primitive proposition asserting that every couple has a relation holding between no other pairs of terms. But it is necessary to give sense to the couple, to distinguish the referent [domain] from the relatum [converse domain]: thus a couple becomes essentially distinct from a class of two terms, and must itself be introduced as a primitive idea. . . . It seems therefore more correct to take an intensional view of relations, and to identify them rather with class-concepts than with classes."[54]
By 1910-1913 and Principia Mathematica Russell had given up on the requirement for an intensional definition of a relation, stating that "mathematics is always concerned with extensions rather than intensions" and "Relations, like classes, are to be taken in extension".[55] To demonstrate the notion of a relation in extension Russell now embraced the notion of ordered couple: "We may regard a relation ... as a class of couples ... the relation determined by φ(x, y) is the class of couples (x, y) for which φ(x, y) is true".[56] In a footnote he clarified his notion and arrived at this definition:
- "Such a couple has a sense, i.e., the couple (x, y) is different from the couple (y, x) unless x = y. We shall call it a "couple with sense," ... it may also be called an ordered couple.[56]
But he goes on to say that he would not introduce the ordered couples further into his "symbolic treatment"; he proposes his "matrix" and his unpopular axiom of reducibility in their place.
An attempt to solve the problem of the antinomies led Russell to propose his "doctrine of types" in an appendix B of his 1903 The Principles of Mathematics.[57] In a few years he would refine this notion and propose in his 1908 The Theory of Types two axioms of reducibility, the purpose of which were to reduce (single-variable) propositional functions and (dual-variable) relations to a "lower" form (and ultimately into a completely extensional form); he and Alfred North Whitehead would carry this treatment over to Principia Mathematica 1910-1913 with a further refinement called "a matrix".[58] The first axiom is *12.1; the second is *12.11. To quote Wiener the second axiom *12.11 "is involved only in the theory of relations".[59] Both axioms, however, were met with skepticism and resistance; see more at Axiom of reducibility. By 1914 Norbert Wiener, using Whitehead and Russell's symbolism, eliminated axiom *12.11 (the "two-variable" (relational) version of the axiom of reducibility) by expressing a relation as an ordered pair "using the null set. At approximately the same time, Hausdorff (1914, p. 32) gave the definition of the ordered pair (a, b) as { {a,1}, {b, 2} }. A few years later Kuratowski (1921) offered a definition that has been widely used ever since, namely { {a, b}, {a} }".[60] As noted by Suppes (1960) "This definition . . . was historically important in reducing the theory of relations to the theory of sets.[61]
Observe that while Wiener "reduced" the relational *12.11 form of the axiom of reducibility he did not reduce nor otherwise change the propositional-function form *12.1; indeed he declared this "essential to the treatment of identity, descriptions, classes and relations".[62]
Schönfinkel's notion of "function" as a many-one "correspondence" 1924
Where exactly the general notion of "function" as a many-one relationship derives from is unclear. Russell in his 1920 Introduction to Mathematical Philosophy states that "It should be observed that all mathematical functions result form one-many [sic -- contemporary usage is many-one] relations . . . Functions in this sense are descriptive functions".[63] A reasonable possibility is the Principia Mathematica notion of "descriptive function" -- R 'y =DEF (ιx)(x R y): "the singular object that has a relation R to y". Whatever the case, by 1924, Moses Schonfinkel expressed the notion, claiming it to be "well known":
- "As is well known, by function we mean in the simplest case a correspondence between the elements of some domain of quantities, the argument domain, and those of a domain of function values ... such that to each argument value there corresponds at most one function value".[64]
According to Willard Quine, Schönfinkel's 1924 "provide[s] for ... the whole sweep of abstract set theory. The crux of the matter is that Schönfinkel lets functions stand as arguments. ¶ For Schönfinkel, substantially as for Frege, classes are special sorts of functions. They are propositional functions, functions whose values are truth values. All functions, propositional and otherwise, are for Schönfinkel one-place functions".[65] Remarkably, Schönfinkel reduces all mathematics to an extremely compact functional calculus consisting of only three functions: Constancy, fusion (i.e., composition), and mutual exclusivity. Quine notes that Haskell Curry (1958) carried this work forward "under the head of combinatory logic".[66]
von Neumann's set theory 1925
By 1925 Abraham Fraenkel (1922) and Thoralf Skolem (1922) had amended Zermelo's set theory of 1908. But von Neumann was not convinced that this axiomatization could not lead to the antinomies.[67] So he proposed his own theory, his 1925 An axiomatization of set theory. It explicitly contains a "contemporary", set-theoretic version of the notion of "function":
- "[Unlike Zermelo's set theory] [w]e prefer, however, to axiomatize not "set" but "function". The latter notion certainly includes the former. (More precisely, the two notions are completely equivalent, since a function can be regarded as a set of pairs, and a set as a function that can take two values.)".[68]
His axiomatization creates two "domains of objects" called "arguments" (I-objects) and "functions" (II-objects); where they overlap are the "argument functions" (I-II objects). He introduces two "universal two-variable operations" -- (i) the operation [x, y]: ". . . read 'the value of the function x for the argument y) and (ii) the operation (x, y): ". . . (read 'the ordered pair x, y'") whose variables x and y must both be arguments and that itself produces an argument (x,y)". To clarify the function pair he notes that "Instead of f(x) we write [f,x] to indicate that f, just like x, is to be regarded as a variable in this procedure". And to avoid the "antinomies of naive set theory, in Russell's first of all . . . we must forgo treating certain functions as arguments".[69] He adopts a notion from Zermelo to restrict these "certain functions"[70]
Since 1950
Notion of "function" in contemporary set theory
Both axiomatic and naive forms of Zermelo's set theory as modified by Fraenkel (1922) and Skolem (1922) define "function" as a relation, define a relation as a set of ordered pairs, and define an ordered pair as a set of two "dissymetric" sets.
While the reader of Suppes (1960) Axiomatic Set Theory or Halmos (1970) Naive Set Theory observes the use of function-symbolism in the axiom of separation, e.g., φ(x) (in Suppes) and S(x) (in Halmos), they will see no mention of "proposition" or even "first order predicate calculus". In their place are "expressions of the object language", "atomic formulae", "primitive formulae", and "atomic sentences".
Kleene 1952 defines the words as follows: "In word languages, a proposition is expressed by a sentence. Then a 'predicate' is expressed by an incomplete sentence or sentence skeleton containing an open place. For example, "___ is a man" expresses a predicate ... The predicate is a propositional function of one variable. Predicates are often called 'properties' ... The predicate calculus will treat of the logic of predicates in this general sense of 'predicate', i.e., as propositional function".[71]
The reason for the disappearance of the words "propositional function" e.g., in Suppes (1960), and Halmos (1970), is explained by Alfred Tarski 1946 together with further explanation of the terminology:
- "An expression such as x is an integer, which contains variables and, on replacement of these variables by constants becomes a sentence, is called a SENTENTIAL [i.e., propositional cf his index] FUNCTION. But mathematicians, by the way, are not very fond of this expression, because they use the term "function" with a different meaning. ... sentential functions and sentences composed entirely of mathematical symbols (and not words of everyday languange), such as: x + y = 5 are usually referred to by mathematicians as FORMULAE. In place of "sentential function" we shall sometimes simply say "sentence" --- but only in cases where there is no danger of any misunderstanding".[72]
For his part Tarski calls the relational form of function a "FUNCTIONAL RELATION or simply a FUNCTION" .[73] After a discussion of this "functional relation" he asserts that:
- "The concept of a function which we are considering now differs essentially from the concepts of a sentential [propositional] and of a designatory function .... Strictly speaking ... [these] do not belong to the domain of logic or mathematics; they denote certain categories of expressions which serve to compose logical and mathematical statements, but they do not denote things treated of in those statements... . The term "function" in its new sense, on the other hand, is an expression of a purely logical character; it designates a certain type of things dealt with in logic and mathematics."[74]
See more about "truth under an interpretation" at Alfred Tarski.
Further developments
The idea of structure-preserving functions, or homomorphisms, led to the abstract notion of morphism, the key concept of category theory. More recently, the concept of functor has been used as an analogue of a function in category theory.[75]
See also
|
|
|
Notes
- ↑ 1.0 1.1 The history of the function concept in mathematics J.P.Ponte, 1992
- ↑ Another short but useful history is found in Eves 1990 pages 234-235
- ↑ Thompson, S.P; Gardner, M; Calculus Made Easy. 1998. Page 10-11. ISBN 0312185480.
- ↑ Eves dates Leibniz's first use to the year 1694 and also similarly relates the usage to "as a term to denote any quantity connected with a curve, such as the coordinates of a point on the curve, the slope of the curve, and so on" (Eves 1990:234).
- ↑ Eves 1990:234
- ↑ 6.0 6.1 Eves 1990:235
- ↑ Eves asserts that Dirichlet "arrived at the following formulation: "[The notion of] a variable is a symbol that represents any one of a set of numbers; if two variables x and y are so related that whenever a value is assigned to x there is automatically assigned, by some rule or correspondence, a value to y, then we say y is a (single-valued) function of x. The variable x . . . is called the independent variable and the variable y is called the dependent variable. The permissible values that x may assume constitute the domain of definition of the function, and the values taken on by y constitute the range of values of the function . . . it stresses the basic idea of a relationship between two sets of numbers" Eves 1990:235.
- ↑ Boole circa 1849 Elementary Treatise on Logic not mathematical including philosophy of mathematical reasoning in Grattan-Guiness and Bornet 1997:40
- ↑ De Morgan 1847:1
- ↑ Boole 1848 in Grattan-Guiness and Bornet 1997:1, 2
- ↑ Boole 1848 in Grattan-Guiness and Bornet 1997:6
- ↑ Eves 1990:222
- ↑ Some of this criticism is intense: see the introduction by Willard Quine preceding Russell 1908 Mathematical logic as based on the theory of types in van Heijenoort 1967:151. See also von Neumann's introduction to his 1925 Axiomatization of Set Theory in van Heijenoort 1967:395
- ↑ Boole 1854:86
- ↑ cf Boole 1854:31-34. Boole discusses this "special law" with its two algebraic roots x = 0 or 1, on page 37.
- ↑ Although he gives others credit, cf Venn 1881:6
- ↑ Venn 1881: 86-87
- ↑ cf van Heijenoort's introduction to Peano 1889 in van Heijenoort 1967. For most of his logical symbolism and notions of propositions Peano credits "many writers, especially Boole". In footnote 1 he credits Boole 1847, 1848, 1854, Schröder 1877, Peirce 1880, Jevons 1883, MacColl 1877, 1878, 1878a, 1880; cf van Heijenoort 1967:86).
- ↑ Frege 1879 in van Heijenoort 1967:7
- ↑ Frege's exact words are "expressed in our formula language" and "expression", cf Frege 1879 in van Heijenoort 1967:21-22.
- ↑ This example is from Frege 1879 in van Heijenoort 1967:21-22
- ↑ Frege 1879 in van Heijenoort 1967:21-22
- ↑ Frege cautions that the function will have "argument places" where the argument should be placed as distinct from other places where the same sign might appear. But he does not go deeper into how to signify these positions and Russell 1903 observes this.
- ↑ Gottlob Frege (1879) in van Heijenoort 1967:21-24
- ↑ "...Peano intends to cover much more ground than Frege does in his Begriffsschrift and his subsequent works, but he does not till that ground to any depth comparable to what Frege does in his self-allotted field", van Heijenoort 1967:85
- ↑ van Heijenoort 1967:89.
- ↑ van Heijenoort 1967:91.
- ↑ All symbols used here are from Peano 1889 in van Heijenoort 1967:91).
- ↑ cf van Heijenoort 1967:91
- ↑ "In Mathematics, my chief obligations, as is indeed evident, are to Georg Cantor and Professor Peano. If I had become acquainted sooner with the work of Professor Frege, I should have owed a great deal to him, but as it is I arrived independently at many results which he had already established", Russell 1903:viii. He also highlights Boole's 1854 Laws of Thought and Ernst Schröder's three volumes of "non-Peanesque methods" 1890, 1891, and 1895 cf Russell 1903:10
- ↑ 31.0 31.1 31.2 Russell 1903:505
- ↑ Russell 1903:5-6
- ↑ Russell 1903:7
- ↑ Russell 1903:19
- ↑ Russell 1910-1913:15
- ↑ Whitehead and Russell 1910-1913:6, 8 respectively
- ↑ Something similar appears in Tarski 1946. Tarski refers to a "relational function" as a "ONE-MANY [sic!] or FUNCTIONAL RELATION or simply a FUNCTION". Tarski comments about this reversal of variables on page 99.
- ↑ Whitehead and Russell 1910-1913:31. This paper is important enough that van Heijenoort reprinted it as Whitehead and Russell 1910 Incomplete symbols: Descriptions with commentary by W. V. Quine in van Heijenoort 1967:216-223
- ↑ Kleene 1952:53
- ↑ Hilbert in van Heijenoort 1967:466
- ↑ Turing 1936-7 in Martin Davis The Undecidable 1965:145
- ↑ cf Kleene 1952:45
- ↑ "The nonprimitive and arbitrary character of this axiom drew forth severe criticism, and much of subsequent refinement of the logistic program lies in attempts to devise some method of avoiding the disliked axiom of reducibility" Eves 1990:268.
- ↑ Frege 1879 in van Heijenoort 1967:23
- ↑ Russell (1902) Letter to Frege in van Heijenoort 1967:124
- ↑ Frege (1902) Letter to Russell in van Heijenoort 1967:127
- ↑ van Heijenoort's commentary to Russell's Letter to Frege in van Heijenoort 1967:124
- ↑ The original uses an Old High German symbol in place of Φ cf Zermelo 1908a in van Heijenoort 1967:202
- ↑ Zermelo 1908a in van Heijenoort 1967:203
- ↑ cf van Heijenoort's commentary before Zermelo 1908 Investigations in the foundations of set theory I in van Heijenoort 1967:199
- ↑ Skolem 1922 in van Heijenoort 1967:292-293
- ↑ van Heijenoort's introduction to Abraham Fraenkel's The notion "definite" and the independence of the axiom of choice in van Heijenoort 1967:285.
- ↑ But Wiener offers no date or reference cf Wiener 1914 in van Heijenoort 1967:226
- ↑ Russell 1903:99
- ↑ both quotes from Whitehead and Russell 1913:26
- ↑ 56.0 56.1 Whitehead and Russell 1913:26
- ↑ Russell 1903:523-529
- ↑ *12 The Hierarchy of Types and the axiom of Reducibility in Principia Mathematica 1913:161
- ↑ Wiener 1914 in van Heijenoort 1967:224
- ↑ commentary by van Heijenoort preceding Norbert Wiener's (1914) A simplification of the logic of relations in van Heijenoort 1967:224.
- ↑ Suppes 1960:32. This same point appears in van Heijenoort's commentary before Wiener (1914) in van Heijenoort 1967:224.
- ↑ Wiener 1914 in van Heijeoort 1967:224
- ↑ Russell 1920:46
- ↑ Schönfinkel (1924) On the building blocks of mathematical logic in van Heijenoort 1967:359
- ↑ commentary by W. V. Quine preceding Schönfinkel (1924) On the building blocks of mathematical logic in van Heijenoort 1967:356.
- ↑ cf Curry and Feys 1958; Quine in van Heijenoort 1967:357.
- ↑ von Neumann's critique of the history observes the split between the logicists (e.g., Russell et. al.) and the set-theorists (e.g., Zermelo et. al.) and the formalists (e.g., Hilbert), cf von Neumann 1925 in van Heijenoort 1967:394-396.
- ↑ von Neumann 1925 in van Heijenoort 1967:396
- ↑ All quotes from von Neumann 1925 in van Heijenoort 1967:397-398
- ↑ This notion is not easy to summarize; see more at van Heijenoort 1967:397.
- ↑ Kleene 1952:143-145
- ↑ Tarski 1946:5
- ↑ Tarski 1946:98
- ↑ Tarski 1946:102
- ↑ John C. Baez; James Dolan (1998). Categorification. http://arxiv.org/abs/math/9802029.
References
- Anton, Howard (1980), Calculus with Analytical Geometry, Wiley, ISBN 978-0-471-03248-9
- Bartle, Robert G. (1976), The Elements of Real Analysis (2nd ed.), Wiley, ISBN 978-0-471-05464-1
- Husch, Lawrence S. (2001), Visual Calculus, University of Tennessee, http://archives.math.utk.edu/visual.calculus/, retrieved 2007-09-27
- Katz, Robert (1964), Axiomatic Analysis, D. C. Heath and Company.
- Ponte, João Pedro (1992), "The history of the concept of function and some educational implications", The Mathematics Educator 3 (2): 3–8, ISSN 1062-9017, http://www.math.tarleton.edu/Faculty/Brawner/550%20MAED/History%20of%20functions.pdf
- Thomas, George B.; Finney, Ross L. (1995), Calculus and Analytic Geometry (9th ed.), Addison-Wesley, ISBN 978-0-201-53174-9
- Youschkevitch, A. P. (1976), "The concept of function up to the middle of the 19th century", Archive for History of Exact Sciences 16 (1): 37–85, doi:10.1007/BF00348305.
- Monna, A. F. (1972), "The concept of function in the 19th and 20th centuries, in particular with regard to the discussions between Baire, Borel and Lebesgue", Archive for History of Exact Sciences 9 (1): 57–84, doi:10.1007/BF00348540.
- Kleiner, Israel (1989), "Evolution of the Function Concept: A Brief Survey", The College Mathematics Journal (Mathematical Association of America) 20 (4): 282–300, doi:10.2307/2686848, http://jstor.org/stable/2686848.
- Ruthing, D. (1984), "Some definitions of the concept of function from Bernoulli, Joh. to Bourbaki, N.", Mathematical Intelligencer 6 (4): 72–77.
- Dubinsky, Ed; Harel, Guershon (1992), The Concept of Function: Aspects of Epistemology and Pedagogy, Mathematical Association of America, ISBN 0883850818.
- Malik, M. A. (1980), "Historical and pedagogical aspects of the definition of function", International Journal of Mathematical Education in Science and Technology 11 (4): 489–492, doi:10.1080/0020739800110404.
- Boole, George (1854), An Investigation into the Laws of Thought on which are founded the Laws of Thought and Probabilities", Walton and Marberly, London UK; Macmillian and Company, Cambridge UK. Republished as a googlebook.
- Eves, Howard. (1990), Fundations and Fundamental Concepts of Mathematics: Third Edition, Dover Publications, Inc. Mineola, NY, ISBN 0-486-69609-X (pbk)
- Frege, Gottlob. (1879), Begriffsschrift: eine der arithmetischen nachgebildete Formelsprache des reinen Denkens, Halle
- Grattan-Guinness, Ivor and Bornet, Gérard (1997), George Boole: Selected Manuscripts on Logic and its Philosophy, Springer-Verlag, Berlin, ISBN 3-7643-5456-9 (Berlin...)
- Halmos, Paul R. (1970) Naive Set Theory, Springer-Verlag, New York, ISBN 0-387-90092-6.
- Hardy, Godfrey Harold (1908), A Course of Pure Mathematics, Cambridge University Press (published 1993), ISBN 978-0-521-09227-2
- Reichenbach, Hans (1947) Elements of Symbolic Logic, Dover Publishing Inc., New York NY, ISBN 0-486-24004-5.
- Russell, Bertrand (1903) The Principles of Mathematics: Vol. 1, Cambridge at the University Press, Cambridge, UK, republished as a googlebook.
- Russell, Bertrand (1920) Introduction to Mathematical Philosophy (second edition), Dover Publishing Inc., New York NY, ISBN 0-486-27724-0 (pbk).
- Suppes, Patrick (1960) Axiomatic Set Theory, Dover Publications, Inc, New York NY, ISBN 0-486-61630-4. cf his Chapter 1 Introduction.
- Tarski, Alfred (1946) Introduction to Logic and to the Methodolgy of Deductive Sciences, republished 1195 by Dover Publications, Inc., New York, NY ISBN 0-486-28462-x
- Venn, John (1881) Symbolic Logic, Macmillian and Co., London UK. Republished as a googlebook.
- van Heijenoort, Jean (1967, 3rd printing 1976), From Frege to Godel: A Source Book in Mathematical Logic, 1879-1931, Harvard University Press, Cambridge, MA, ISBN 0-674-32449-8 (pbk)
- Gottlob Frege (1879) Begriffsschrift, a formula language, modeled upon that of arithmetic, for pure thought with commentary by van Heijenoort, pages 1–82
- Giuseppe Peano (1889) The principles of arithmetic, presented by a new method with commentary by van Heijenoort, pages 83–97
- Bertrand Russell (1902) Letter to Frege with commentary by van Heijenoort, pages 124-125. Wherein Russell announces his discovery of a "paradox" in Frege's work.
- Gottlob Frege (1902) Letter to Russell with commentary by van Heijenoort, pages 126-128.
- David Hilbert (1904) On the foundations of logic and arithmetic, with commentary by van Heijenoort, pages 129-138.
- Jules Richard (1905) The principles of mathematics and the problem of sets, with commentary by van Heijenoort, pages 142-144. The Richard paradox.
- Bertrand Russell (1908a) Mathematical logic as based on the theory of types, with commentary by Willard Quine, pages 150-182.
- Ernst Zermelo (1908) A new proof of the possibility of a well-ordering, with commentary by van Heijenoort, pages 183-198. Wherein Zermelo rales against Poincaré's (and therefore Russell's) notion of impredicative definition.
- Ernst Zermelo (1908a) Investigations in the foundations of set theory I, with commentary by van Heijenoort, pages 199-215. Wherein Zermelo attempts to solve Russell's paradox by structuring his axioms to restrict the universal domain B (from which objects and sets are pulled by definite properties) so that it itself cannot be a set, i.e., his axioms disallow a universal set.
- Norbert Wiener (1914) A simplification of the logic of relations, with commentary by van Heijenoort, pages 224-227
- Thoralf Skolem (1922) Some remarks on axiomatized set theory, with commentary by van Heijenoort, pages 290-301. Wherein Skolem defines Zermelo's vague "definite property".
- Moses Schönfinkel (1924) On the building blocks of mathematical logic, with commentary by Willard Quine, pages 355-366. The start of combinatory logic.
- John von Neumann (1925) An axiomatization of set theory, with commentary by van Heijenoort , pages 393-413. Wherein von Neumann creates "classes" as distinct from "sets" (the "classes" are Zermelo's "definite properties"), and now there is a universal set, etc.
- David Hilbert (1927) The foundations of mathematics by van Heijenoort, with commentary, pages 464-479.
- Whitehead, Alfred North and Russell, Bertrand (1913, 1962 edition), Principia Mathematica to *56, Cambridge at the University Press, London UK, no ISBN or US card catalog number.
External links
- The Wolfram Functions Site gives formulae and visualizations of many mathematical functions.
- Shodor: Function Flyer, interactive Java applet for graphing and exploring functions.
- xFunctions, a Java applet for exploring functions graphically.
- Draw Function Graphs, online drawing program for mathematical functions.
- Functions from cut-the-knot.
- Function at ProvenMath.
- Comprehensive web-based function graphing & evaluation tool